Bresenham의 라인 알고리즘이란 무엇입니까?
- Bresenham Line Algorithm은 복잡하고 계산 속도가 느린 실수를 포함하는 계산을 제외하고 정수 계산만을 사용하여 직선을 그리기 위해 컴퓨터 그래픽에서 개발된 알고리즘입니다.
Bresenham 직선 알고리즘을 사용하는 이유는 무엇입니까?
- 직선을 그릴 때 직선 방정식 ‘y = mx + b’를 사용하여 그릴 수 있습니다. 그러나 이러한 직선 방정식을 그대로 플로팅하려면 실수를 사용해야 합니다. 예전에는 실수연산의 성능이 좋지 않아서 최대한 정수연산만 사용했는데, 픽셀단위로 직선을 그릴때는 브레젠햄 직선알고리즘을 사용하는 것이 더 적절하다. 실수가 있는 직선 방정식 대신 정수만 있는 직선. .
Bresenham 라인 알고리즘의 원리
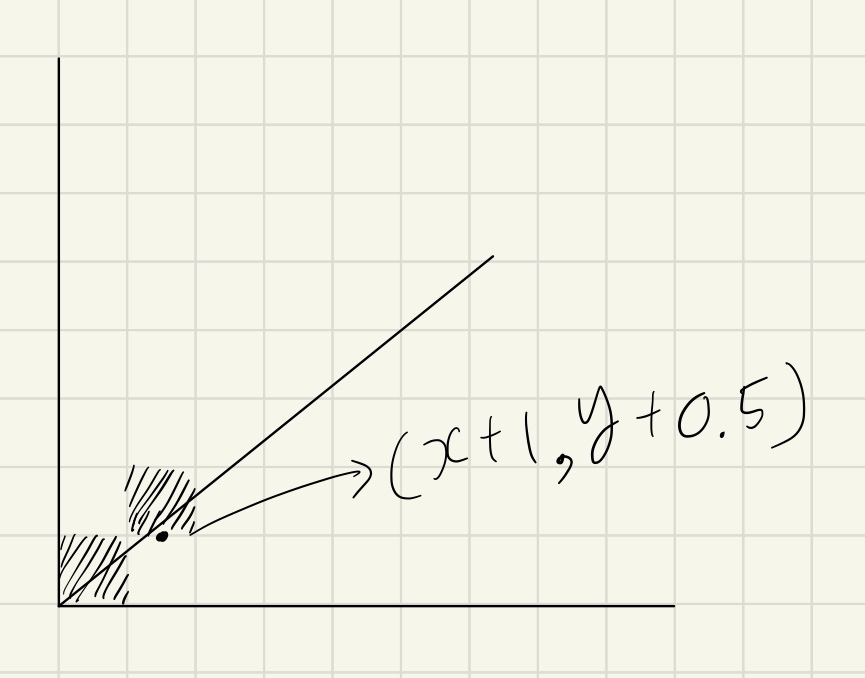
- Bresenham의 직선 알고리즘에서 위와 같이 기울기가 0보다 크고 1보다 작고(x0 + 1, y0 + 0.5) 선이 좌표 위에 있으면 y축의 픽셀 위치가 1만큼 증가하고 그 이하이면 증가하지 않습니다. 한 점에 한 픽셀씩 그립니다.
기울기가 0보다 크고 1보다 작은 경우 Bresenham 라인 알고리즘의 판별식을 찾는 방법
// a는 기울기, b는 y절편입니다.
y = ax + b
// x에는 +1, y에는 +0.5를 합니다.
(y + 0.5) = a(x + 1) + b;
// y절편을 구하는 공식은 y - (h/w)x 입니다.
(h/w)(x + 1) + y - (h/w)x = (y + 0.5)
// y가 더 클 경우 직선이 위에 있고, 더 작을 경우 직선이 아래에 있습니다.
(h/w)(x + 1) + y - (h/w)x < (y + 0.5)
// y의 위치를 옮김니다.
(h/w)(x + 1) + y - (h/w)x - (y + 0.5) < 0
// 각 항에 w를 곱하여 분자를 없앱니다.
h(x + 1) + wy - hx - w(y + 0.5) < 0
// x와 y에 0을 대입하고, 소수점을 없애기 위해서 2를 곱합니다.
2h - w < 0- 위와 같이 기울기에 따라 판별식을 구할 수 있습니다. x가 1씩 증가할 때마다 판별식은 2h씩 증가하고, x와 y 값이 1씩 증가할 때마다 판별식은 2w+2h씩 증가합니다. 즉, 2h – w < 0이 성립하지 않기 때문에 x와 y를 증가시키면 다음 판별식에 사용하기 위해 2h - w를 2h - 2w에 더해야 합니다.
Bresenham의 직선 알고리즘 코드
#include <iostream>
using namespace std;
constexpr int MAX_LEN = 30;
int m(MAX_LEN)(MAX_LEN);
void makeBresenhamLine(int startX, int startY, int endX, int endY)
{
int width = abs(startX - endX);
int height = abs(startY - endY);
int xFactor = startX > endX ? -1 : 1;
int yFactor = startY > endY ? -1 : 1;
if (width > height)
{
int y = startY;
int dest = 2 * height - width;
for (int x = startX; x != endX; x += xFactor)
{
m(y)(x) = 1;
if (dest < 0)
dest += 2 * height;
else
{
y += yFactor;
dest += 2 * height - 2 * width;
}
}
}
else
{
int x = startX;
int dest = 2 * width - height;
for (int y = startY; y != endY; y += yFactor)
{
m(y)(x) = 1;
if (dest < 0)
dest += 2 * width;
else
{
x += xFactor;
dest += 2 * width - 2 * height;
}
}
}
return;
}
int main()
{
int startX, startY, endX, endY;
cout << "시작 좌표와 끝 좌표를 입력해주세요 (x와 y의 최대 크기는 29입니다.)\n";
cin >> startX >> startY >> endX >> endY;
// y좌표 뒤집기
startY = MAX_LEN - startY - 1;
endY = MAX_LEN - endY - 1;
makeBresenhamLine(startX, startY, endX, endY);
for (int y = 0; y < MAX_LEN; ++y) {
for (int x = 0; x < MAX_LEN; ++x) {
cout << m(y)(x) << " ";
}
cout << "\n";
}
return 0;
}